石墨烯模型哈密顿量推导和边界态构建
从原子出发
晶格向量
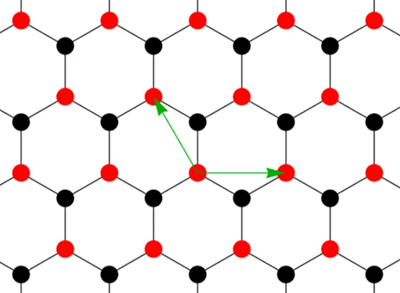
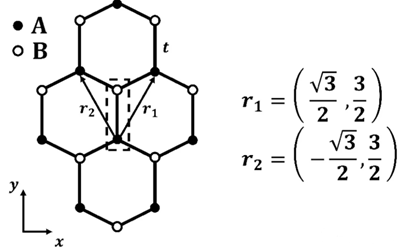
石墨烯的晶格是 Honeycomb Lattice(蜂窝晶格),由两种子格点(A、B)构成。尽管它看起来是六边形,但它实际上是由两个互相嵌套的三角形子晶格形成的 布里渊区(Brillouin Zone)。
定义晶格矢量:每个原胞中有两种子格a和b(红色和黑色),晶格矢量记为v1和v1:
v1=(3,0)
v2=(−23,23)
紧束缚哈密顿量
考虑最近邻,哈密顿量为:
H=−t⟨i,j⟩∑ai†bj−t⟨i,j⟩∑bi†aj
ai†表示产生算符,bj表示湮灭算符,一个电子从 ai跃迁到 bj
负号表示能量的减少,跃迁过程会降低系统的总能量,因此在哈密顿量中引入了负号,表示这种能量的降低。
石墨烯中a和b就是最近邻,它们互有三个最近邻,写为:
H=−ti∑ai†bi+e1−ti∑ai†bi+e2−ti∑ai†bi+e3+h.c
h.c表示复共轭
其中最近邻矢量为:
e1=(0,1)
e2=(−23,−21)
e3=(23,−21)
这三个矢量描述了从 A 原子到最近邻 B 原子的跃迁方向,从最近邻矢量写出实空间哈密顿量然后傅立叶变换可以写出倒空间哈密顿量。
傅里叶变换形式
对算符进行傅里叶变换:
ak=N1i∑aieik⋅r
ai=N1k∑ake−ik⋅r
bk=N1i∑bieik⋅r
bi=N1k∑bke−ik⋅r
通过傅里叶变换,可以得到:
−ti∑ari†bri+e1=−tk∑ak†bke−ik⋅e1
−ti∑ari†bri+e2=−tk∑ak†bke−ik⋅e2
−ti∑ari†bri+e3=−tk∑ak†bke−ik⋅e3
哈密顿量写成完整形式:
H=−tk∑(ak†bke−ik⋅e1+ak†bke−ik⋅e2+ak†bke−ik⋅e3)−tk∑(bk†akeik⋅e1+bk†akeik⋅e2+bk†akeik⋅e3)
写成矩阵形式为:
H=k∑(ak†bk†)(0H21H120)(akbk)
H12=−t(e−ik⋅e1+e−ik⋅e2+e−ik⋅e3)
H21=−t(eik⋅e1+eik⋅e2+eik⋅e3)
原胞思想求解
直接求解是通过傅里叶变换来推导,原胞方法是另一种构建哈密顿量的方法,它先将整个晶格划分成原胞,然后考虑原胞之间的相互作用。
基本思路
原胞思想是通过将整个系统分解为基本单元(原胞)来求解哈密顿量的方法。相比直接求解方法,这种方法更加直观和系统化。
哈密顿量的基本形式
H=−t⟨i,j⟩∑ci†cj+h.c.
其中⟨i,j⟩表示最近邻跃迁,这种表示和之前的 −t∑⟨i,j⟩ai†bj−t∑⟨i,j⟩bi†aj 完全一样。
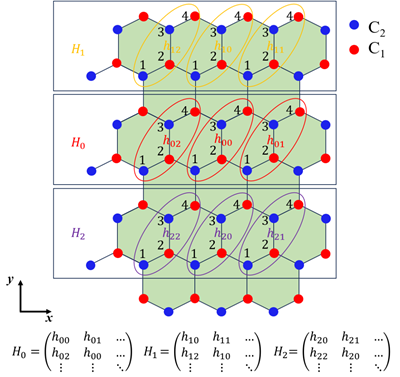
原胞构造
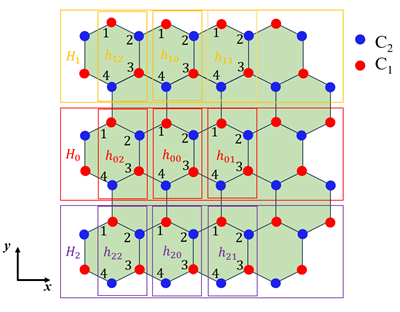
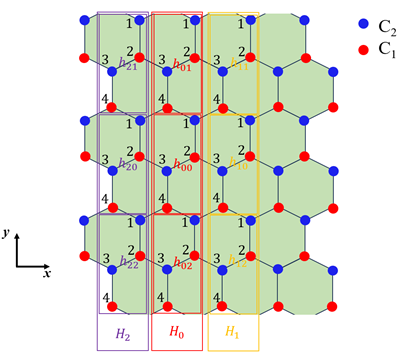
系统中有两种不同的碳原子,用黑色(A)和白色(B)标识。将这两个原子打包成一个结构基元,用算符表示为:
ψi†=(ci,a†ci,b†)
这样只需要看这一个基元里面的跃迁和相邻位置的跃迁。用A原子代表整个原胞的位置,图中 r₁,r₂是每个原胞到相邻原胞的矢量。
求解步骤
第一步:原胞自己到自己的矩阵,写成:
(ci,a†ci,b†)(Ha,aHb,aHa,bHb,b)(ci,aci,b)
A到A(或B到B)跃迁为0,因为在位能为0,所以 Ha,a=Hb,b=0。来回跃迁的hopping为 t,所以:
Ha,b=Hb,a=t
H00=(0tt0)
(原胞内部中最近邻原子的跃迁,取 i=0,ψ0†=(c0,a†,c0,b†),所以矩阵表示为 H00)
(ci,a†ci,b†)(Ha,aHb,aHa,bHb,b)(ci,aci,b)=Haaci,a†ci,a+Habci,a†ci,b+Hbaci,b†ci,a+Hbbci,b†ci,b
其中的跃迁对应为
Haa:a→aHab:a→bHba:b→aHbb:b→b
第二步:相邻原胞到这个原胞的跃迁矩阵,这里为原胞自己到近邻,也就是从0到1或2(即A通过 r1或 r2跃迁,并且下边两个相反的取厄米共轭),基元中A到相邻原胞A跃迁不是最近邻,所以应该是相邻原胞中A原子到基元中B原子的跃迁。如0到1,矩阵写成
(c1,a†c0,b†)(HaaHbaHabHbb)(c1,ac0,b)
0到2类似,所以
H01=H02=(0t00)
第三步:将每个矩阵乘上e指数相加,就得到哈密顿量的核了,所以
H=H00+(H01eikr1+H02eikr2+h.c.)
也就是
H=(0t(1+e−ikr1+e−ikr2)t(1+eikr1+eikr2)0)
写成 d向量模式
H=dx(k)σx+dy(k)σy
其中
{dx(k)=t(1+cos(kr1)+cos(kr2))dy(k)=t(sin(kr1)+sin(kr2))
Honeycomb lattice的傅里叶变换(FT)两种规范
六角晶格由两个子格子A和B组成,每个原胞包含这两个不同的site。最近邻跃迁的傅里叶变换可以用两种规范来描述。
第一种规范
FT的变换因子直接基于A、B点的具体位置。得到的哈密顿量 H(k) 不满足布里渊区的周期边条件 H(k)=H(k+G)
ari=N1k∑ake−ik⋅ri,bri=N1k∑bke−ik⋅ri
第二种规范
对B点进行修正,将其视为与同一原胞内A点位置相同的点。这种方法确保 H(k)=H(k+G)哈密顿量满足周期性。
两种规范下能带(色散关系)一致,但第一种规范下的波函数不满足布里渊区的周期性,因此在计算拓扑不变量(如陈数)时需要额外考虑边界贡献。
ari=N1k∑ake−ik⋅ri,bri=N1k∑bke−ik⋅(ri−τ)
其中B的FT变换因子里多了一项τ=(a,0)=e3是A到B的平移矢量。B的坐标减去τ就是同一原胞内A的坐标。也就是说,在这种规范下,只把原胞的位置(即A的位置)作为FT的变换因子,忽略原胞内部细节,将B视为与A处于同一位置。这相当于做了规范变换 bk→bkeik⋅e3,不影响物理可观测量(比如能带)。
直接求解是第一种规范,原胞求解是第二种规范
边界态
石墨烯常见的三种边缘态,分别为锯齿(zigzag)型、扶手椅(armchair)型和胡须(bearded)型边缘态。
armchair边缘态
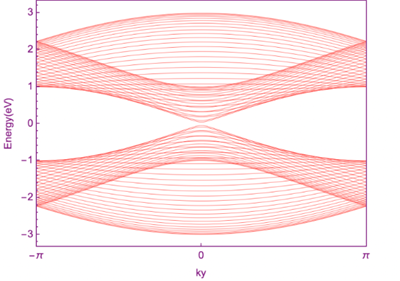
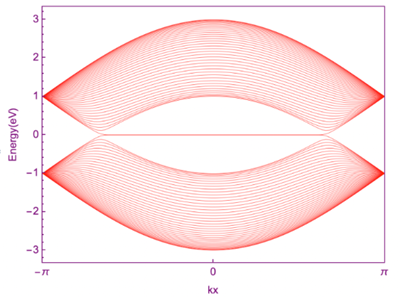
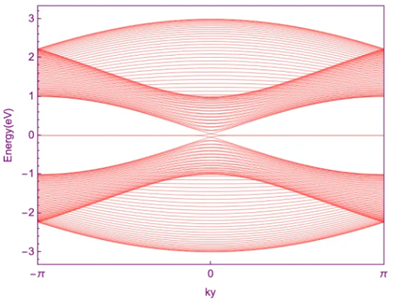
对于石墨烯的armchair边缘态,要求y方向为周期性,x方向为有限层。
bearded边缘态
石墨烯的bearded边缘态,x方向为周期性,y方向为有限层
石墨烯的第四种边缘态-桠型(twig)边缘态
参考资料
https://mp.weixin.qq.com/s/fj888DpJ56wdbgbwvrBc6Q
https://zhuanlan.zhihu.com/p/92538964