Haldane模型

Haldane模型是由F. D. Haldane在1988年提出的，它描述了蜂窝晶格上带有次近邻复数相位的电子运动。

Haldane模型的关键：

质量项：在两个子晶格（通常记为a和b）上施加不同的能量，从而打破反演对称性。
最近邻跃迁：与石墨烯类似，电子在相邻的a和b子晶格间跃迁，跃迁幅度为 $t_1$ ，次近邻跃迁：电子在相同子晶格内部的跃迁，同时在跃迁过程中引入复数相位 $e^{i\psi_{ij}\phi}$（其中相位正负取决于跃迁路径的方向），该项打破时间反演对称性，但总磁通为零，从而实现了量子反常霍尔效应。

直接求解

$$H = M \sum_i \xi_i c_i^\dagger c_i + t_1 \sum_{\langle i,j \rangle} c_i^\dagger c_j + t_2 \sum_{\langle \langle i,j \rangle \rangle} e^{i \psi_{ij} \phi} c_i^\dagger c_j + \text{h.c.}$$

$<i,j>$是最近邻跃迁，$<<i,j>>$是次近邻跃迁

质量项

$$\xi_i=\pm 1$$

其中 $\xi_i=\pm1$对应两个子晶格。这一项在能带结构中引入了能量不对称性，决定了系统处于拓扑平凡或非平凡相。

最近邻跃迁项

类似于石墨烯

$$H_{NN}=t_1 \sum_k \left( a_k^\dagger b_k e^{-i k \cdot e_1} + a_k^\dagger b_k e^{-i k \cdot e_2} + a_k^\dagger b_k e^{-i k \cdot e_3} \right) + t_1 \sum_k \left( b_k^\dagger a_k e^{i k \cdot e_1} + b_k^\dagger a_k e^{i k \cdot e_2} + b_k^\dagger a_k e^{i k \cdot e_3} \right)$$

其中

$$e_1 = (0, 1), e_2 = \left( -\frac{\sqrt{3}}{2}, -\frac{1}{2} \right), e_3 = \left( \frac{\sqrt{3}}{2}, -\frac{1}{2} \right)$$

这部分与石墨烯模型相似，构造了两个子晶格之间的直接耦合。

次近邻跃迁项

第三项为引入交替磁通后次近邻的跃迁，a到a跃迁和b到b跃迁的相位$\phi$相反

$$H_{NNN}= t_2 e^{i \phi} \sum_i a_{r_i}^\dagger a_{r_i + v_i} - t_2 e^{i \phi} \sum_i a_{r_i + v_i}^\dagger a_{r_i - v_3} + t_2 e^{i \phi} \sum_i a_{r_i - v_3}^\dagger a_{r_i} + \text{h.c.} + (a \to b, \phi \rightarrow -\phi)$$

其中

$$v_1 = (\sqrt{3}, 0)，v_2 = \left(-\frac{\sqrt{3}}{2}, \frac{3}{2}\right)，v_3 = \left(-\frac{\sqrt{3}}{2}, -\frac{3}{2}\right)$$

对 $H_{NNN}$，注意到其环路跃迁等价于中心原子a沿着$v1、v2、v3$跃迁，所以有

$$H_{NNN}=t_2e^{i\phi}\sum_{i}a_{r_i}^{\dagger}a_{r_{i+\nu_1}}+t_2e^{i\phi}\sum_{i}a_{r_i}^{\dagger}a_{r_{i+\nu_2}}+t_2e^{i\phi}\sum_{i}a_{r_i}^{\dagger}a_{r_{i+\nu_3}}+\text{h.c.}+(a\to b,\phi\to -\phi)$$

傅立叶变换后，得到

$$\begin{aligned} H_{NNN}&=t_2e^{i\phi}\sum_{k}a_{k}^{\dagger}a_{k}(e^{-i\boldsymbol{k}\cdot\boldsymbol{v}_1}+e^{-i\boldsymbol{k}\cdot\boldsymbol{v}_2}+e^{-i\boldsymbol{k}\cdot\boldsymbol{v}_3})+\text{h.c.}+(a\to b,\phi\to -\phi)\\ &=2t_2\sum_{k}a_{k}^{\dagger}a_{k}[\cos(\boldsymbol{k}\cdot\boldsymbol{v}_1 - \phi)+\cos(\boldsymbol{k}\cdot\boldsymbol{v}_2 - \phi)+\cos(\boldsymbol{k}\cdot\boldsymbol{v}_3 - \phi)]+\\ &2t_2\sum_{k}b_{k}^{\dagger}b_{k}[\cos(\boldsymbol{k}\cdot\boldsymbol{v}_1+\phi)+\cos(\boldsymbol{k}\cdot\boldsymbol{v}_2+\phi)+\cos(\boldsymbol{k}\cdot\boldsymbol{v}_3+\phi)] \end{aligned}$$

这个项在整个晶格内形成闭合的环路跃迁，其复数相位的符号依赖于环路的方向（顺时针或逆时针），这正是实现拓扑性质的关键。

原胞思想求解

$$H = M \sum_i \xi_i c_i^\dagger c_i + t_1 \sum_{\langle i,j \rangle} c_i^\dagger c_j + t_2 \sum_{\langle \langle i,j \rangle \rangle} e^{i \psi_{ij} \phi} c_i^\dagger c_j + \text{h.c.}$$

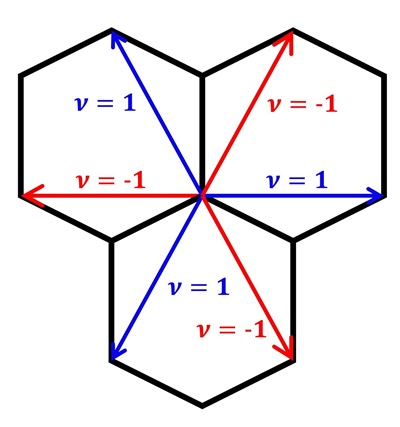
对第三项的$v_{ij}$，如果电子从 $j$到 $i$，中间要经过两条六边形的边，这两个边的单位矢量分别是$\boldsymbol{d}{j}$，$\boldsymbol{d}{k}$，那么就有

$$v_{ij}=\frac{2}{\sqrt{3}}\boldsymbol{d}{j}\times\boldsymbol{d}{k}=\pm1$$

构造原胞Hamiltonian矩阵

自己到自己，得到

$$H_{00}=\begin{pmatrix} M & t_1\\ t_1 & -M \end{pmatrix}$$

也就是顺时针转取正，逆时针转取负。

接下来考虑其它原胞到本原胞的跃迁，例如：

$$H_{01}=\begin{pmatrix} t_2e^{i\phi}&0\\ 0&t_2e^{-i\phi} \end{pmatrix} H_{02}=\begin{pmatrix} t_2e^{i\phi}&0\\ t_1&t_2e^{-i\phi} \end{pmatrix} H_{03}=\begin{pmatrix} t_2e^{i\phi}&t_1\\ 0&t_2e^{-i\phi} \end{pmatrix}$$

这里$H_{01}$表示相邻原胞1到原先原胞0跃迁，$H_{02}$、$H_{03}$ 类似。

这些矩阵描述了不同方向的原胞间耦合。加入傅里叶因子 $e^{i\boldsymbol{k}\cdot\boldsymbol{v}_i}$后，整体Hamiltonian写为

$$H = H_{00}+(H_{01}e^{i\boldsymbol{k}\cdot\boldsymbol{v}_1}+H_{02}e^{i\boldsymbol{k}\cdot\boldsymbol{v}_2}+H_{03}e^{i\boldsymbol{k}\cdot\boldsymbol{v}_3}+\text{h.c.})$$

最终的Hamiltonian矩阵

$$\begin{aligned} H&=\begin{pmatrix} M + h_{11}&h_{12}\\ h_{21}&-M + h_{22} \end{pmatrix}\\ \end{aligned}$$

$$\begin{aligned} \begin{cases} h_{11}&=t_2\left(e^{i(kv_1+\phi)}+e^{i(kv_2+\phi)}+e^{i(kv_3+\phi)}+e^{-i(kv_1+\phi)}+e^{-i(kv_2+\phi)}+e^{-i(kv_3+\phi)}\right)\\ &=2t_2\left(\cos(kv_1+\phi)+\cos(kv_2+\phi)+\cos(kv_3+\phi)\right)\\ h_{12}&=t_1\left(1 + e^{ikv_2}+e^{-ikv_2}\right)\\ h_{21}&=t_1\left(1 + e^{ikv_2}+e^{-ikv_2}\right)\\ h_{22}&=t_2\left(e^{i(kv_1 - \phi)}+e^{i(kv_2 - \phi)}+e^{i(kv_3 - \phi)}+e^{-i(kv_1 - \phi)}+e^{-i(kv_2 - \phi)}+e^{-i(kv_3 - \phi)}\right)\\ &=2t_2\left(\cos(kv_1 - \phi)+\cos(kv_2 - \phi)+\cos(kv_3 - \phi)\right) \end{cases} \end{aligned}$$

这样就得到了一个关于波矢 $\boldsymbol{k}$ 的2×2矩阵，便于进一步求解能带结构。

能带

利用上面的Hamiltonian矩阵，我们可以直接求解其本征值，即能带。

通过数值求解或解析求根，可以得到系统的能带图像（附件中的图像展示了不同参数下能带的分布），其中可以看到因 $t_2$与相位 $\phi$引入的拓扑非平庸性，系统出现带隙并伴随非零的拓扑不变量。

边界态

为了研究边界态，需要构造有限尺寸系统的Hamiltonian，将系统按原胞层级展开，写成类似分块矩阵的形式：

$$H_{00}=\begin{pmatrix} T_0&T_y&\cdots\\ T_y^{\dagger}&T_0&\cdots\\ \vdots&\vdots&\ddots \end{pmatrix}$$

其中 $T_0$表示原胞内部的Hamiltonian，其具体矩阵可以写为

$$T_0=\begin{pmatrix} M&t_1&t_2e^{-i\phi}&0\\ t_1&-M&t_1&t_2e^{-i\phi}\\ t_2e^{i\phi}&t_1&M&t_1\\ 0&t_2e^{i\phi}&t_1&-M \end{pmatrix}$$

$T_y$表示沿垂直方向（例如y方向）的跃迁矩阵：

$$T_y=\begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ t_2e^{i\phi}&0&0&0\\ t_1&t_2e^{i\phi}&0&0 \end{pmatrix}$$

$$H_{01}=\begin{pmatrix} T_x&T_{yx}&\cdots\\ T_{xy}&T_x&\cdots\\ \vdots&\vdots&\ddots \end{pmatrix}$$

$T_{yx}$和 $T_{xy}$是不一样的

$$T_x=\begin{pmatrix} t_2e^{i\phi}&0&0&0\\ t_1&t_2e^{-i\phi}&0&t_2e^{i\phi}\\ t_2e^{-i\phi}&0&t_2e^{i\phi}&t_1\\ 0&0&0&t_2e^{-i\phi} \end{pmatrix}$$

$$T_{yx}=\begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ t_2e^{-i\phi}&0&0&0\\ 0&0&0&0 \end{pmatrix} T_{xy}=\begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&t_2e^{i\phi}&0\\ 0&0&0&0 \end{pmatrix}$$

构造出整个块状矩阵后，边界态的求解便转化为求解这一大矩阵的本征值问题。通常可以通过数值方法获得。

zigzag边缘态

armchair边缘态

总结

Haldane模型利用质量项、最近邻和带相位的次近邻跃迁构成Hamiltonian，展示了在无净磁通条件下实现量子反常霍尔效应的可能。通过选取合适的原胞，将Hamiltonian写成2×2矩阵形式，再利用傅里叶变换处理晶格对称性，可以直接求出能带结构。模型的非平庸拓扑性质在能带求解和边界态分析中均有所体现，不同边界（如zigzag和armchair）的态分布证明了bulk-boundary对应原理。

参考资料

https://mp.weixin.qq.com/s/JvxrsOJjI8w5GoZrskwJwg
https://www.guanjihuan.com/archives/410