双圆偏振光（BCPL, Bicircularly Polarized Light）情况下有效哈密顿量推导

BCPL 数学描述

BCPL 是由两个频率比为整数 $\eta$ 且偏振相反的圆偏振光（CL, Circularly Polarized Light）束叠加

而成的

两个 CL 光束的特点：频率比 $\eta$ 是整数，即其中一个 CL 的角频率为 $\omega$ ，另一个则为 $\eta \omega$ 。偏振相反，即一个是左手圆偏振光（LCP），另一个是右手圆偏振光（RCP）。

光场向量势（vector potential）可以表示为：

\mathbf{A}(t)=\sqrt{2}A_0 \mathrm{Re}\left(e^{-i(\eta\omega t - \alpha)}\hat{\varepsilon}_R + e^{i\omega t}\hat{\varepsilon}_L\right)

$A_0$ 是振幅参数， $\eta$ 是两个 CL 频率的比值（整数）， $\theta$ 是 CL 之间的相对相位。

$\hat{\varepsilon}_1,\hat{\varepsilon}_2$ 分别表示右手圆偏振（RCP, Right Circularly Polarized）和左手圆偏振（LCP, Left Circularly Polarized）

在正交单位向量 $\hat{\varepsilon}_1$ 和 $\hat{\varepsilon}_2$ 的基底上，圆偏振的定义如下：

\hat{\varepsilon}_R = \frac{1}{\sqrt{2}}(\hat{\varepsilon}_1 - i\hat{\varepsilon}_2), \quad \hat{\varepsilon}_L = \frac{1}{\sqrt{2}}(\hat{\varepsilon}_1 + i\hat{\varepsilon}_2)

BCPL 的向量势表达式

BCPL 是由两个 CPL 叠加得到的，它的向量势 $\mathbf{A}(t)$ 在分量形式上写作：

A_1(t) = A_0 \left(r\cos(\eta\omega t - \alpha)+\cos(\omega t)\right)\\ A_2(t) = A_0 \left(-r\sin(\eta\omega t - \alpha)+\sin(\omega t)\right)

$\alpha$ 是相对相位，它的作用是整体角度偏移（angular shift）。

不同的相对振幅 $r$ 值会导致向量势的轨迹呈现不同的模式。

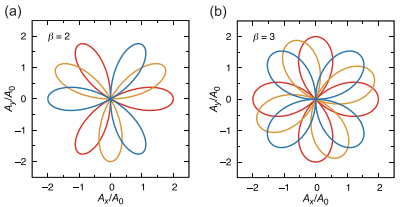
$\alpha$ 仅仅会导致整体角度旋转，但不会改变轨迹的基本形状。

考虑BCPL之后，与施加单圆偏振光情况类似，带入Floquet公式中：

H(\mathbf{k})\to H(\mathbf{k}+e\mathbf{A}(t))

H(t+T)=H(t)

H_m=\frac{1}{T}\int_{0}^{T}dt H(t)e^{-im\omega t}

\begin{aligned} H_F(\boldsymbol{k})&=\sum_{l = 0}^{\infty}H_F^{(l)}(\boldsymbol{k})\\ H_F^{(0)}(\boldsymbol{k})&=H_{0,0}(\boldsymbol{k})\\ H_F^{(1)}(\boldsymbol{k})&=\sum_{i\neq0}\frac{[H_{-i}(\boldsymbol{k}), H_{i}(\boldsymbol{k})]}{2i\omega}\\ H_F^{(2)}(\boldsymbol{k})&=\sum_{i\neq0}\frac{[[H_{-i}(\boldsymbol{k}), H_{0,0}(\boldsymbol{k})], H_{i}(\boldsymbol{k})]}{2i^{2}\omega^{2}}\\ &+\sum_{i\neq0}\sum_{j\neq0}\frac{[[H_{-i}(\boldsymbol{k}), H_{i - j}(\boldsymbol{k})], H_{j}(\boldsymbol{k})]}{3ij\omega^{2}} \end{aligned}

利用公式

e^{iu\sin(\Omega t+\theta)}=\sum_{l = -\infty}^{\infty}\mathcal{J}_l(u)e^{il(\Omega t+\theta)}

将 $H(k,t)$ 中含时指数项替换成级数展开形式，然后对 $e^{il(\Omega t+\theta)}$ 积分。避免直接对 $e^{iu\sin(\Omega t+\theta)}$ 求解。

以该文献中其中一项为例

t_{ij}^{AB}(t)=t_{\text{NN}}e^{-iu\sin(\Omega t-\frac{2\pi}{3}r_{ij})}e^{iu\sin(\beta\Omega t-\theta+\frac{2\pi}{3}r_{ij})}

替换系数然后积分得到

t_{\text{eff}}^{(AB)}(\mathbf{R}i - \mathbf{R}j)=t_{\text{NN}}\sum_{l = -\infty}^{\infty}\mathcal{J}_{\beta l}(u)\mathcal{J}l(u)e^{-il\theta}e^{i(\beta + 1)l\frac{2\pi}{3}r{ij}}

与单圆偏振光一项只包含一个第一类贝塞尔函数形式不同的是积分后包含两个贝塞尔函数相乘。

对于得到的结果按按需求截断（一般情况只需要考虑前1~2阶，可以自行数值计算后判断保留到哪一阶）。

该文献通过在类似石墨烯的中心对称系统施加BCPL，实现谷选择霍尔效应，是首个展示 BCPL 诱导谷选择性霍尔效应的研究。